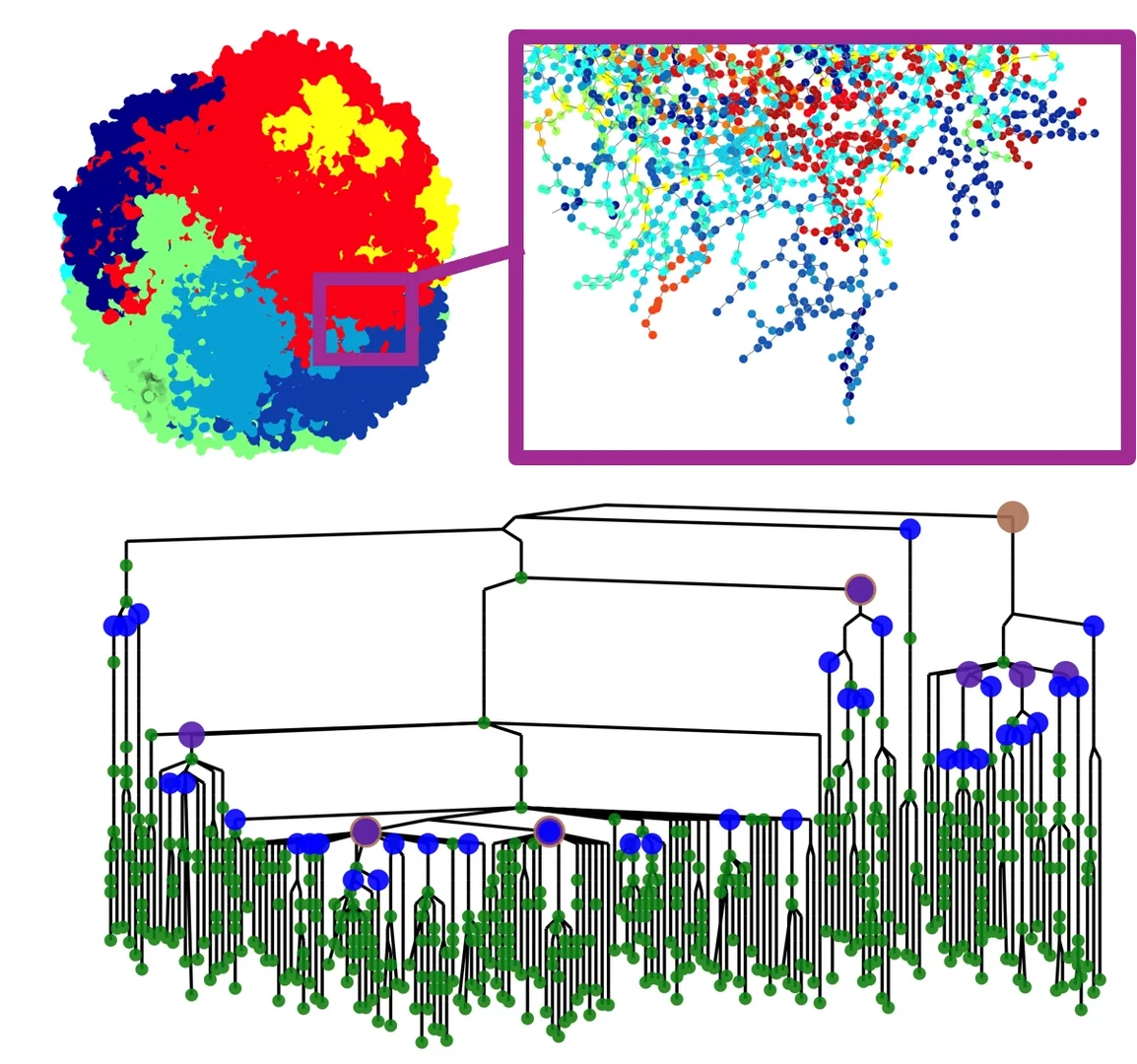
Das Team hat Prostatatumore untersucht und mit Hilfe von mathematischer Modellierung ein konzeptionell durchdachtes, realistisches, dreidimensionales Modell des Prostatakrebses entwickelt. Das Modell bildet Tumorwachstum, genetische Evolution und den Konkurrenzkampf zwischen Subklonen - unterschiedliche Zellpopulationen innerhalb eines Tumors - ab. Das Modell zeigt unter anderem, dass für die Entwicklung eines aggressiven Tumors sogenannte „starke“ genetische Veränderungen erforderlich sind, die den Tumorzellen auf einen Schlag besondere Überlebensvorteile verleihen. Diese müssen früh im Verlauf der Tumorentwicklung auftreten, wenn der Tumor noch klein ist. Die Studie zeigt zudem, dass die Verteilung der Subklone innerhalb eines Tumors Einfluss auf diagnostische Ansätze wie Biopsien hat.
Prostatakrebs ist die häufigste Krebserkrankung bei Männern. Die Mechanismen der Tumorentwicklung, insbesondere hin zu aggressiven Tumoren, sind jedoch bei Prostatakrebs und anderen bösartigen Tumoren noch weitgehend unklar. Zwei Hauptgründe tragen zu diesem Wissensmangel bei. Erstens werden Tumore oft erst entdeckt, wenn sie bereits eine beträchtliche Größe erreicht haben. Die Zeitspanne zwischen der Entstehung des Tumors und dem Zeitpunkt der Diagnose, manchmal 10–30 Jahre, bleibt somit unberücksichtigt. Zweitens sind moderne Methoden, wie das Next-Generation-Sequencing (NGS), die eine umfassende Charakterisierung des Tumors auf Ebene der Subklone ermöglichen, kostspielig und in der Auswertung äußerst komplex. Aufgrund dieser Einschränkungen konnten bisher weltweit nur wenige Tumore auf diese Weise untersucht werden.
„Unsere Studie zeigt, dass wir mit mathematischer Modellierung wichtige, bisher ungeklärte Fragen zur Entwicklung von bösartigen Tumoren angehen und damit klinisch relevante Einblicke gewinnen können. Unser Modell ist universell einsetzbar und kann auch auf andere maligne Tumortypen angewendet werden“, erklärt der Oberarzt und Ko-Leiter der Studie, Privatdozent Dr. Yuri Tolkach vom Institut für Allgemeine Pathologie und Pathologische Anatomie der Uniklinik Köln.
„Mit unserem neuen Modell können wir die komplexe räumliche Struktur eines Prostatakrebses, der wie eine Art Wurzelsystem im Gewebe liegt, nachbilden“, erläutert der Postdoc und Ko-Leiter der Studie, Dr. Florian Kreten, der am Institut für Angewandte Mathematik der Universität Bonn tätig war und nun am Uniklinikum in Köln forscht. Er ergänzt: „Gängige mathematische Modelle von Tumorwachstum und -evolution ließen sich auf diese Strukturen nicht anwenden. Aus mathematischer Sicht ist der zugrundeliegende Wachstumsmechanismus äußerst faszinierend und hat einige neue Fragestellungen aufgeworfen. Die Arbeit zeigt, wie die Biologie die mathematische Forschung inspirieren kann.“ In Zukunft hoffen die Wissenschaftler, die Modelle noch weiterentwickeln und um die Interaktion zwischen Tumor und Immunsystem erweitern zu können.